テストで平均点を取った時、「だいたい真ん中位の順位だった」と思っていませんでしたか。
確かに平均というと「真ん中」。多くも少なくもなくというイメージです。しかし、実はそうとは限りません。
得られる情報が多くなっている現代では、今後、ますますデータを読み解く力が重要になっていきます。つまりデータを正しく見る力の、生活やビジネスにおける重要性がさらに増していくのです。
この記事では、データを扱う上で知っておくべき基本知識である「平均値」「中央値」「最頻値」それぞれの意味と、利用する時の注意点を解説します。
目次
「平均値」と実感が違うケースは多い

テストで平均点を取っても順位が下位になる?
先日このような投稿がTwitterで話題になりました。
その投稿は、
「うちの子は平均より上の点数なのに、クラス内順位がこんなに下なのはおかしい!」
という親からのクレームに対し、先生が平均の計算方法から説明して納得して帰ってもらったという内容でした。
この投稿には「先生大変ですね…」という投稿も多かったのですが、中には「私もその親のように感じてしまう。どうしてそんなことが起こるんですか?」という疑問も多くありました。
平均給与441万円、平均貯蓄1,752万円は高すぎる?
国税庁の民間給与実態調査によると、平成30年における日本人の平均年収は約441万円でした。
また総務省が発表している家計調査報告によると、平成30年の2人以上世帯における貯蓄現在高の平均値は1,752万円です。
このような平均値が発表されると話題になるのが「平均が高すぎる」「自分の周りにそんなに貯蓄できている人はいない」という反応です。
もちろん、その人が住む地域や性別・年代によって年収はかなり違います。
また人は同じくらいの生活レベルの人と接することが自然と多くなるので、「周りにいないから信じられない」という現象も理解はできます。
しかしこのようなデータを見る時に注意するべきことは、「平均値が本当に全体の真ん中を表しているのか」ということなのです。
平均値とは
平均値は、すべてのデータの値をたしてデータの個数で割った値です。
例えば、10人のクラスでテストの点数が下記のようになった場合、平均点は62点となります。
| 点数 | 人数 |
| 100点 | 2人 |
| 80点 | 3人 |
| 70点 | 2人 |
| 30点 | 1人 |
| 10点 | 1人 |
| 0点 | 1人 |
しかしこの場合、平均点以上の70点を獲得した子どもはクラス内の順位で6位となります。
高得点が多いにも関わらず、10点や0点という極端な点数の生徒もいて、平均値が影響を受けてしまったからです。
このように、平均値は必ずしもその集団の平均・普通・真ん中を示すものではありません。
少数のデータが一気に平均値を押し上げたり押し下げたりする可能性があるのです。
平均値を用いる時は、その集団における値の偏りに注意する必要があります。
平均値が真ん中を示すのは極端な数値が含まれない身長などのデータであり、釣鐘状の左右対称の分布になる(正規分布という)場合だけといえます。
中央値とは
対して、集団のデータを小さい順に並べた時中央に位置する値を「中央値」といいます。
| 点数 | 人数 |
| 100点 | 2人 |
| 80点 | 3人 |
| 70点 | 2人 |
| 30点 | 1人 |
| 10点 | 1人 |
| 0点 | 1人 |
先ほどのテスト点数の集団で考えると、中央値は上から5つ目の80点と下から5つ目の70点の平均である75点となります。
※データが偶数個の場合は中央の2つの数値の平均を中央値とし、データが奇数個の場合は中央の数値がそのまま中央値となります。
中央値は、平均値と違い極端な数字の影響を受けにくい数値です。
問題点としては、全体の数値から算出する数値ではないので、毎年の数字の変化を見る時には正しく変化を反映しない場合があります。
例えば平均年収が下がっている傾向にあるのに、給与の中央値が上がるということも考えられます。
最頻値とは
最頻値とは、データの中で最も頻度が高い値のことです。
| 点数 | 人数 |
| 100点 | 2人 |
| 80点 | 3人 |
| 70点 | 2人 |
| 30点 | 1人 |
| 10点 | 1人 |
| 0点 | 1人 |
このテスト結果においては、最頻値は最も得点者が多い80点となります。
最頻値も極端な数値の影響を受けないので、実感に近い数値となるケースが多いです。
年収のデータなどでは、最頻値を見る(最も多い年収を見る)方が実際の生活レベルに近いと感じられるでしょう。
ただし、最頻と言ってもデータの母数が少なく他のデータの出現回数とたいして変わらない、などの場合は果たしてそれを最頻値としていいものか問題になります。
最頻値はデータの数が多い時に使えるものと考えておきましょう。
データを利用する時の注意

このような基本的なデータの見方を知っていないと、正しいデータからでも誤った結論を出してしまいかねません。
例えば、ある地域における30年女性女性の平均年収「約350万円」を参考にマーケティング施策を考えようと思っても、
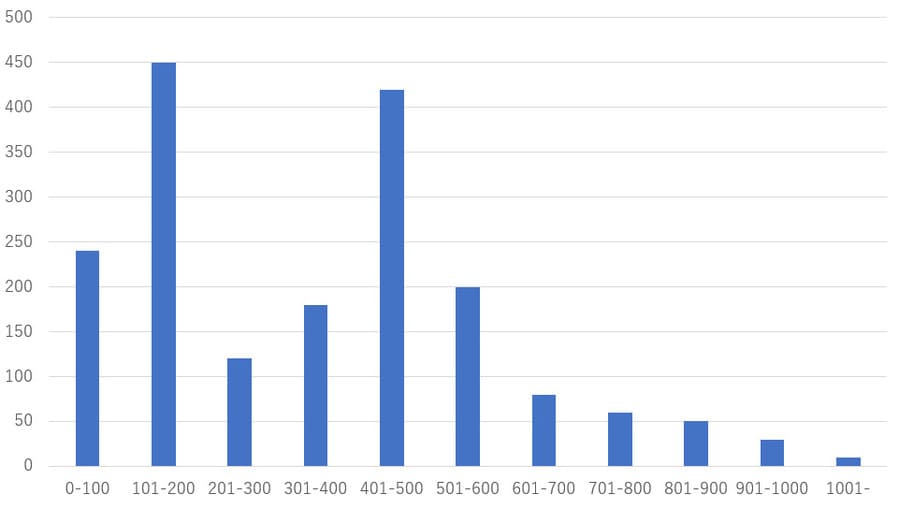
・フルタイムで働き稼いでいる人(平均年収450万円)
・子どもがいてパート勤務の人(平均年収150万円)
に二極化しているとすると、年収350万円の女性は実際には非常に少ないのです。
このように平均や中央値を盲目的に信じると、実態と違った結論や行動に結びつく可能性があります。
各値の特長を理解することが大切

このように、平均値や中央値、最頻値はどれもそのデータの中での「真ん中」示そうとするものですが、算出方法が違い、データの分布によっては実態と違う結果を導いてしまいかねません。
データを扱う時はそれがどんな形に分布しているのか、どのような値を用いると知りたい数値がわかるのか、などを理解する必要があります。
まずは平均と中央値を出して、この2つが乖離していなければ平均が参考になると考えられます。もし乖離していれば、中央値や最頻値も確認してみましょう。



















